publications | Roy T. Forestano

2025

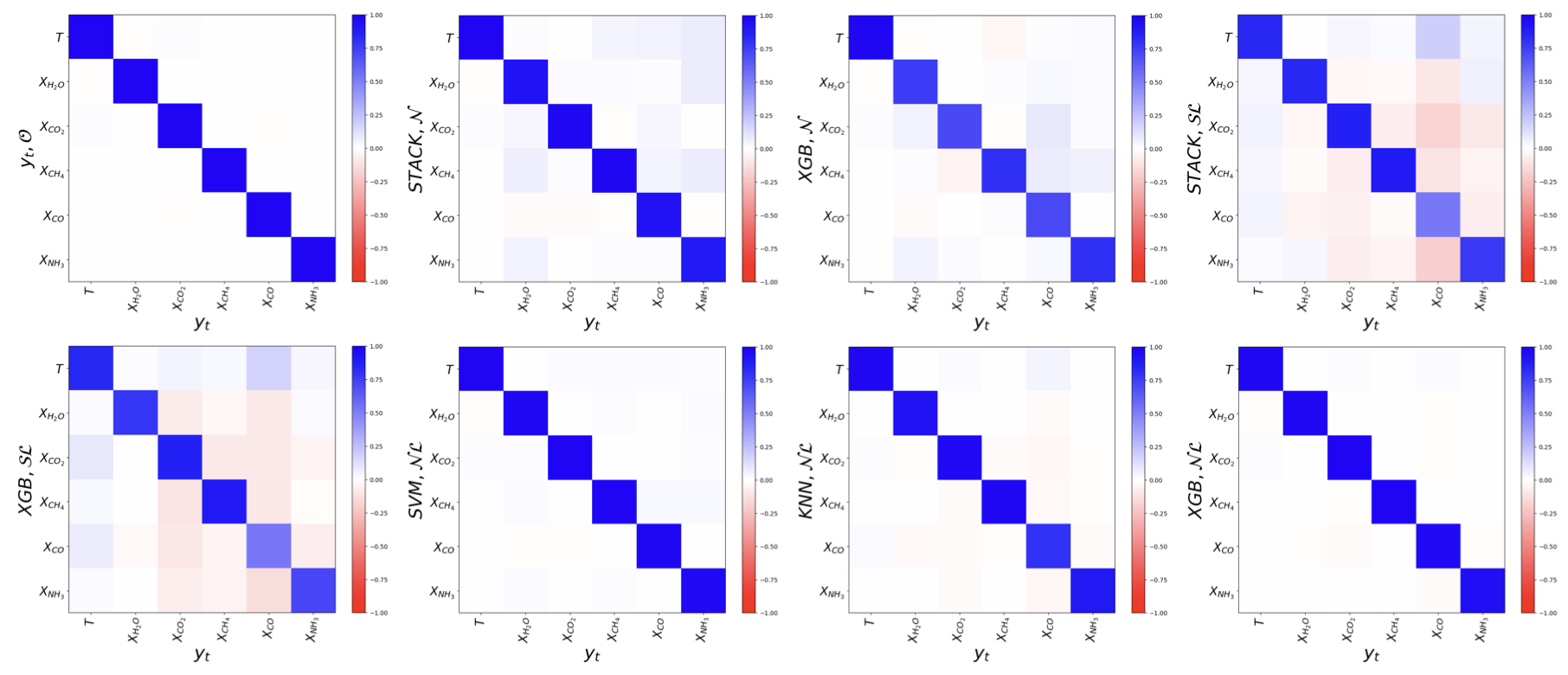Supervised Machine Learning Methods with Uncertainty Quantification for Exoplanet Atmospheric Retrievals from Transmission Spectroscopy

Roy T. Forestano, Konstantin T. Matchev, Katia Matcheva, and 1 more author

2025

Abs PDF

Standard Bayesian retrievals for exoplanet atmospheric parameters from transmission spectroscopy, while well understood and widely used, are generally computationally expensive. In the era of the JWST and other upcoming observatories, machine learning approaches have emerged as viable alternatives that are both efficient and robust. In this paper we present a systematic study of several existing machine learning regression techniques and compare their performance for retrieving exoplanet atmospheric parameters from transmission spectra. We benchmark the performance of the different algorithms on the accuracy, precision, and speed. The regression methods tested here include partial least squares (PLS), support vector machines (SVM), k nearest neighbors (KNN), decision trees (DT), random forests (RF), voting (VOTE), stacking (STACK), and extreme gradient boosting (XGB). We also investigate the impact of different preprocessing methods of the training data on the model performance. We quantify the model uncertainties across the entire dynamical range of planetary parameters. The best performing combination of ML model and preprocessing scheme is validated on a the case study of JWST observation of WASP-39b.
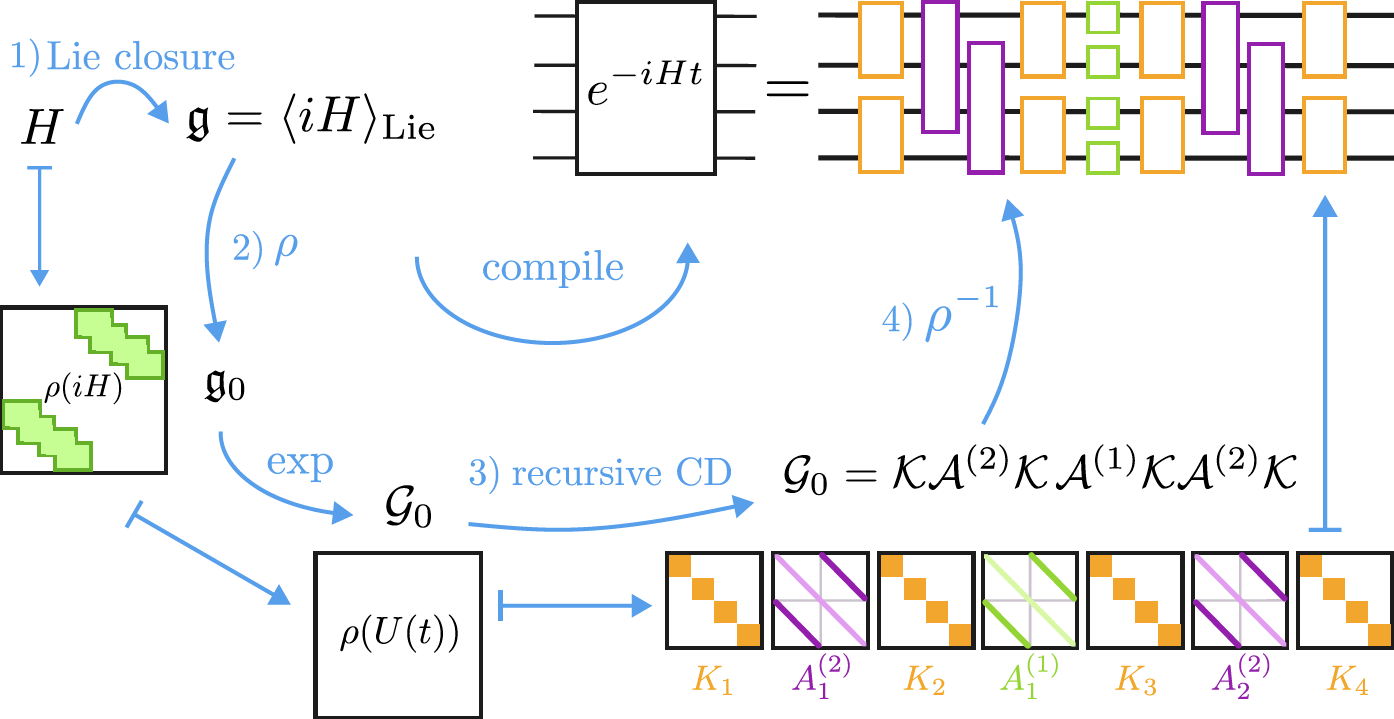Recursive Cartan decompositions for unitary synthesis

David Wierichs, Maxwell West, Roy T. Forestano, and 2 more authors

2025

Abs PDF

Recursive Cartan decompositions (CDs) provide a way to exactly factorize quantum circuits into smaller components, making them a central tool for unitary synthesis. Here we present a detailed overview of recursive CDs, elucidating their mathematical structure, demonstrating their algorithmic utility, and implementing them numerically at large scales. We adapt, extend, and unify existing mathematical frameworks for recursive CDs, allowing us to gain new insights and streamline the construction of new circuit decompositions. Based on this, we show that several leading synthesis techniques from the literature-the Quantum Shannon, Block-ZXZ, and Khaneja-Glaser decompositions-implement the same recursive CD. We also present new recursive CDs based on the orthogonal and symplectic groups, and derive parameter-optimal decompositions. Furthermore, we aggregate numerical tools for CDs from the literature, put them into a common context, and complete them to allow for numerical implementations of all possible classical CDs in canonical form. As an application, we efficiently compile fast-forwardable Hamiltonian time evolution to fixed-depth circuits, compiling the transverse-field XY model on $10^3 qubits into 2 \times 10^6$ gates in 22 seconds on a laptop.

2024

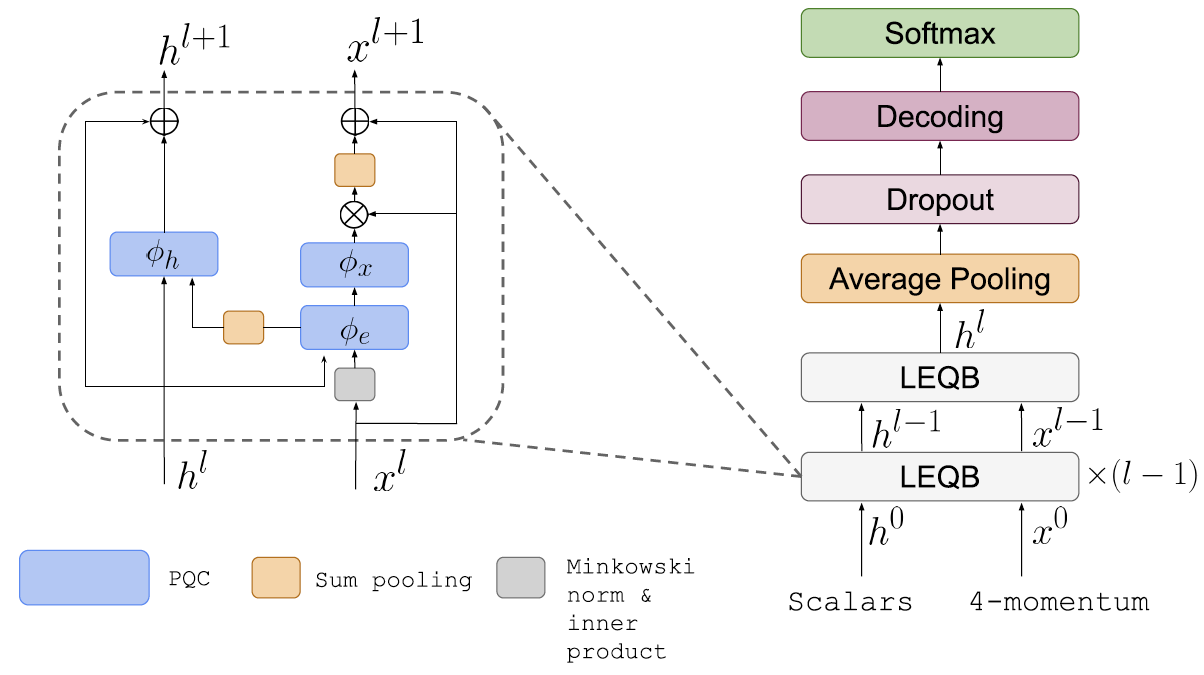Lie-Equivariant Quantum Graph Neural Networks

Jogi Suda Neto, Roy Thomas Forestano, Sergei Gleyzer, and 3 more authors

2024

Abs PDF

Discovering new phenomena at the Large Hadron Collider (LHC) involves the identification of rare signals over conventional backgrounds. Thus binary classification tasks are ubiquitous in analyses of the vast amounts of LHC data. We develop a Lie-Equivariant Quantum Graph Neural Network (Lie-EQGNN), a quantum model that is not only data efficient, but also has symmetry-preserving properties. Since Lorentz group equivariance has been shown to be beneficial for jet tagging, we build a Lorentz-equivariant quantum GNN for quark-gluon jet discrimination and show that its performance is on par with its classical state-of-the-art counterpart LorentzNet, making it a viable alternative to the conventional computing paradigm.
Quantum Vision Transformers for Quark–Gluon Classification

Marçal Comajoan Cara, Gopal Ramesh Dahale, Zhongtian Dong, and 8 more authors

Axioms, 2024

Abs PDF

We introduce a hybrid quantum-classical vision transformer architecture, notable for its integration of variational quantum circuits within both the attention mechanism and the multi-layer perceptrons. The research addresses the critical challenge of computational efficiency and resource constraints in analyzing data from the upcoming High Luminosity Large Hadron Collider, presenting the architecture as a potential solution. In particular, we evaluate our method by applying the model to multi-detector jet images from CMS Open Data. The goal is to distinguish quark-initiated from gluon-initiated jets. We successfully train the quantum model and evaluate it via numerical simulations. Using this approach, we achieve classification performance almost on par with the one obtained with the completely classical architecture, considering a similar number of parameters.
Hybrid Quantum Vision Transformers for Event Classification in High Energy Physics

Eyup B. Unlu, Marçal Comajoan Cara, Gopal Ramesh Dahale, and 8 more authors

Axioms, 2024

Abs PDF

Models based on vision transformer architectures are considered state-of-the-art when it comes to image classification tasks. However, they require extensive computational resources both for training and deployment. The problem is exacerbated as the amount and complexity of the data increases. Quantum-based vision transformer models could potentially alleviate this issue by reducing the training and operating time while maintaining the same predictive power. Although current quantum computers are not yet able to perform high-dimensional tasks, they do offer one of the most efficient solutions for the future. In this work, we construct several variations of a quantum hybrid vision transformer for a classification problem in high-energy physics (distinguishing photons and electrons in the electromagnetic calorimeter). We test them against classical vision transformer architectures. Our findings indicate that the hybrid models can achieve comparable performance to their classical analogs with a similar number of parameters.

2023

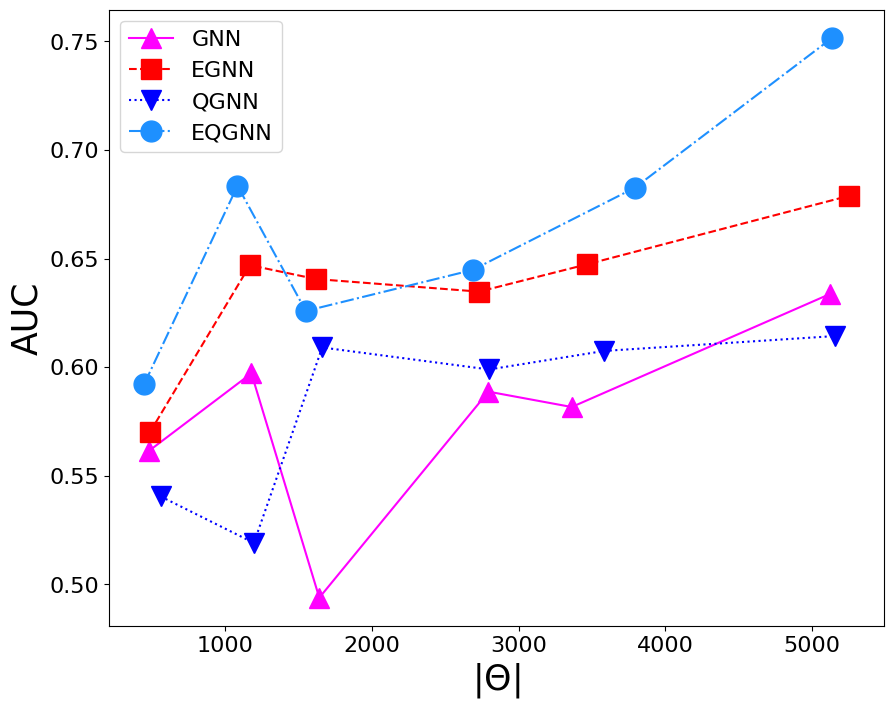A Comparison Between Invariant and Equivariant Classical and Quantum Graph Neural Networks

Roy T. Forestano, Marçal Comajoan Cara, Gopal Ramesh Dahale, and 8 more authors

2023

Abs PDF

Machine learning algorithms are heavily relied on to understand the vast amounts of data from high-energy particle collisions at the CERN Large Hadron Collider (LHC). The data from such collision events can naturally be represented with graph structures. Therefore, deep geometric methods, such as graph neural networks (GNNs), have been leveraged for various data analysis tasks in high-energy physics. One typical task is jet tagging, where jets are viewed as point clouds with distinct features and edge connections between their constituent particles. The increasing size and complexity of the LHC particle datasets, as well as the computational models used for their analysis, greatly motivate the development of alternative fast and efficient computational paradigms such as quantum computation. In addition, to enhance the validity and robustness of deep networks, one can leverage the fundamental symmetries present in the data through the use of invariant inputs and equivariant layers. In this paper, we perform a fair and comprehensive comparison between classical graph neural networks (GNNs) and equivariant graph neural networks (EGNNs) and their quantum counterparts: quantum graph neural networks (QGNNs) and equivariant quantum graph neural networks (EQGNN). The four architectures were benchmarked on a binary classification task to classify the parton-level particle initiating the jet. Based on their AUC scores, the quantum networks were shown to outperform the classical networks. However, seeing the computational advantage of the quantum networks in practice may have to wait for the further development of quantum technology and its associated APIs.
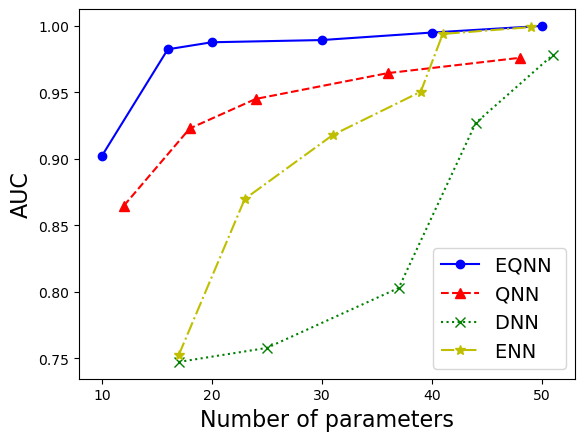Z2 x Z2 Equivariant Quantum Neural Networks: Benchmarking against Classical Neural Networks

Zhongtian Dong, Marçal Comajoan Cara, Gopal Ramesh Dahale, and 8 more authors

2023

Abs PDF

This paper presents a comprehensive comparative analysis of the performance of Equivariant Quantum Neural Networks (EQNN) and Quantum Neural Networks (QNN), juxtaposed against their classical counterparts: Equivariant Neural Networks (ENN) and Deep Neural Networks (DNN). We evaluate the performance of each network with two toy examples for a binary classification task, focusing on model complexity (measured by the number of parameters) and the size of the training data set. Our results show that the Z2 xZ2 EQNN and the QNN provide superior performance for smaller parameter sets and modest training data samples.
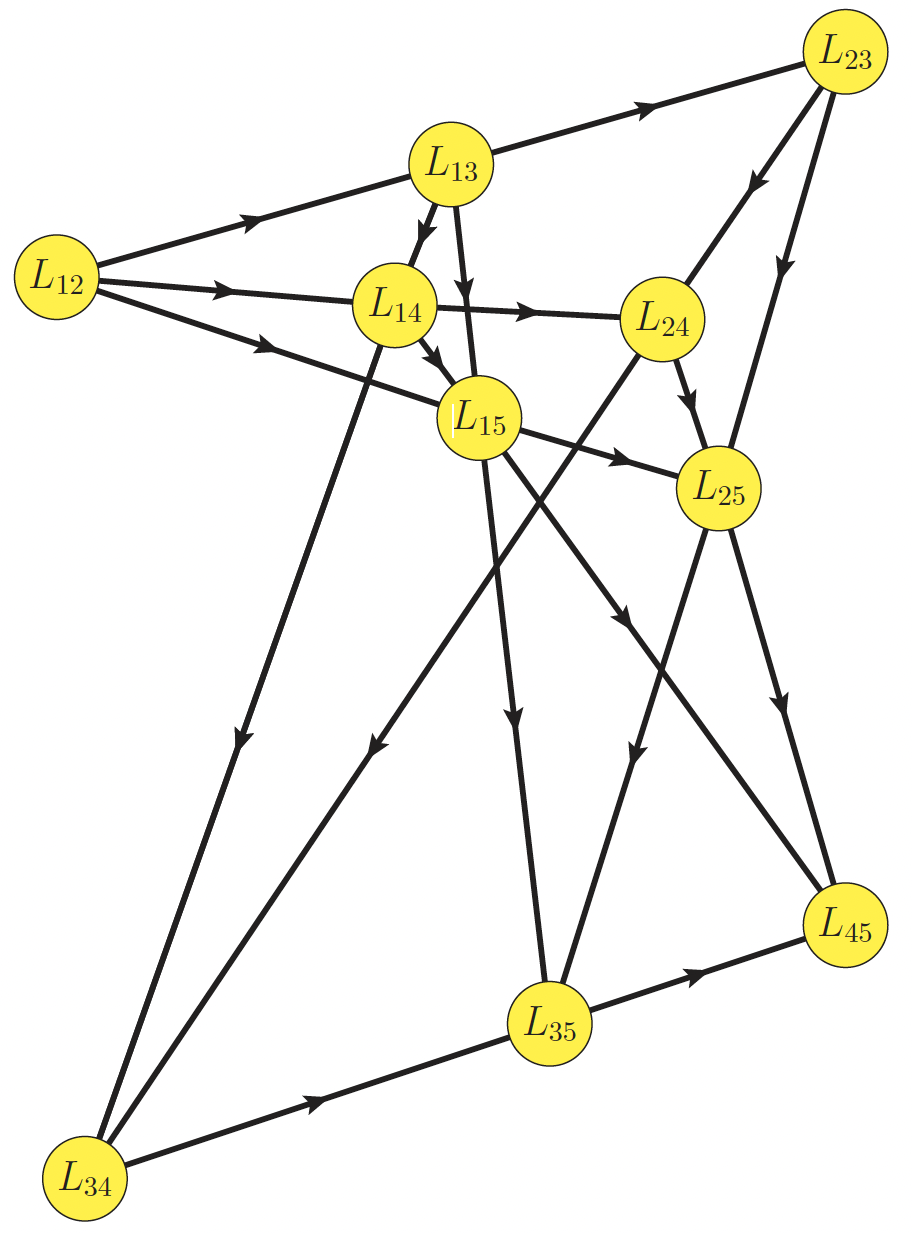Identifying the group-theoretic structure of machine-learned symmetries

Roy T. Forestano, Konstantin T. Matchev, Katia Matcheva, and 3 more authors

Physics Letters B, 2023

Abs PDF

Deep learning was recently successfully used in deriving symmetry transformations that preserve important physics quantities. Being completely agnostic, these techniques postpone the identification of the discovered symmetries to a later stage. In this letter we propose methods for examining and identifying the group-theoretic structure of such machine-learned symmetries. We design loss functions which probe the subalgebra structure either during the deep learning stage of symmetry discovery or in a subsequent post-processing stage. We illustrate the new methods with examples from the U(n) Lie group family, obtaining the respective subalgebra decompositions. As an application to particle physics, we demonstrate the identification of the residual symmetries after the spontaneous breaking of non-Abelian gauge symmetries like SU(3) and SU(5) which are commonly used in model building.
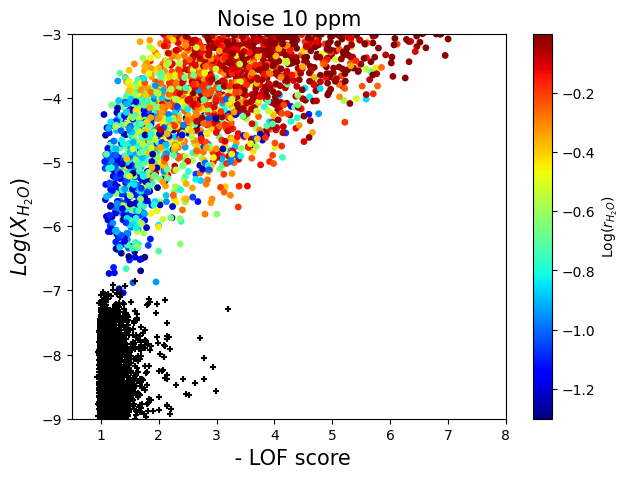Searching for Novel Chemistry in Exoplanetary Atmospheres Using Machine Learning for Anomaly Detection

Roy T. Forestano, Konstantin T. Matchev, Katia Matcheva, and 1 more author

The Astrophysical Journal, Nov 2023

Abs PDF

The next generation of telescopes will yield a substantial increase in the availability of high-quality spectroscopic data for thousands of exoplanets. The sheer volume of data and number of planets to be analyzed greatly motivate the development of new, fast, and efficient methods for flagging interesting planets for reobservation and detailed analysis. We advocate the application of machine learning (ML) techniques for anomaly (novelty) detection to exoplanet transit spectra, with the goal of identifying planets with unusual chemical composition and even searching for unknown biosignatures. We successfully demonstrate the feasibility of two popular anomaly detection methods (local outlier factor and one-class support vector machine) on a large public database of synthetic spectra. We consider several test cases, each with different levels of instrumental noise. In each case, we use receiver operating characteristic curves to quantify and compare the performance of the two ML techniques.
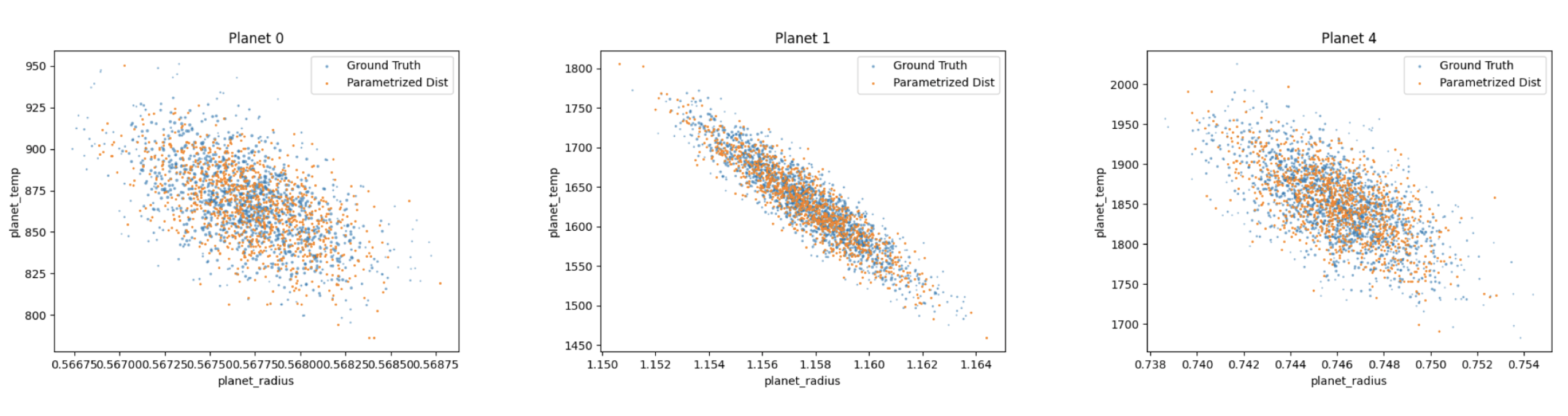Reproducing Bayesian Posterior Distributions for Exoplanet Atmospheric Parameter Retrievals with a Machine Learning Surrogate Model

Eyup B. Unlu, Roy T. Forestano, Konstantin T. Matchev, and 1 more author

Nov 2023

Abs PDF

We describe a machine-learning-based surrogate model for reproducing the Bayesian posterior distributions for exoplanet atmospheric parameters derived from transmission spectra of transiting planets with typical retrieval software such as TauRex. The model is trained on ground truth distributions for seven parameters: the planet radius, the atmospheric temperature, and the mixing ratios for five common absorbers: H2O, CH4, NH3, CO and CO2. The model performance is enhanced by domain-inspired preprocessing of the features and the use of semi-supervised learning in order to leverage the large amount of unlabelled training data available. The model was among the winning solutions in the 2023 Ariel Machine Learning Data Challenge.
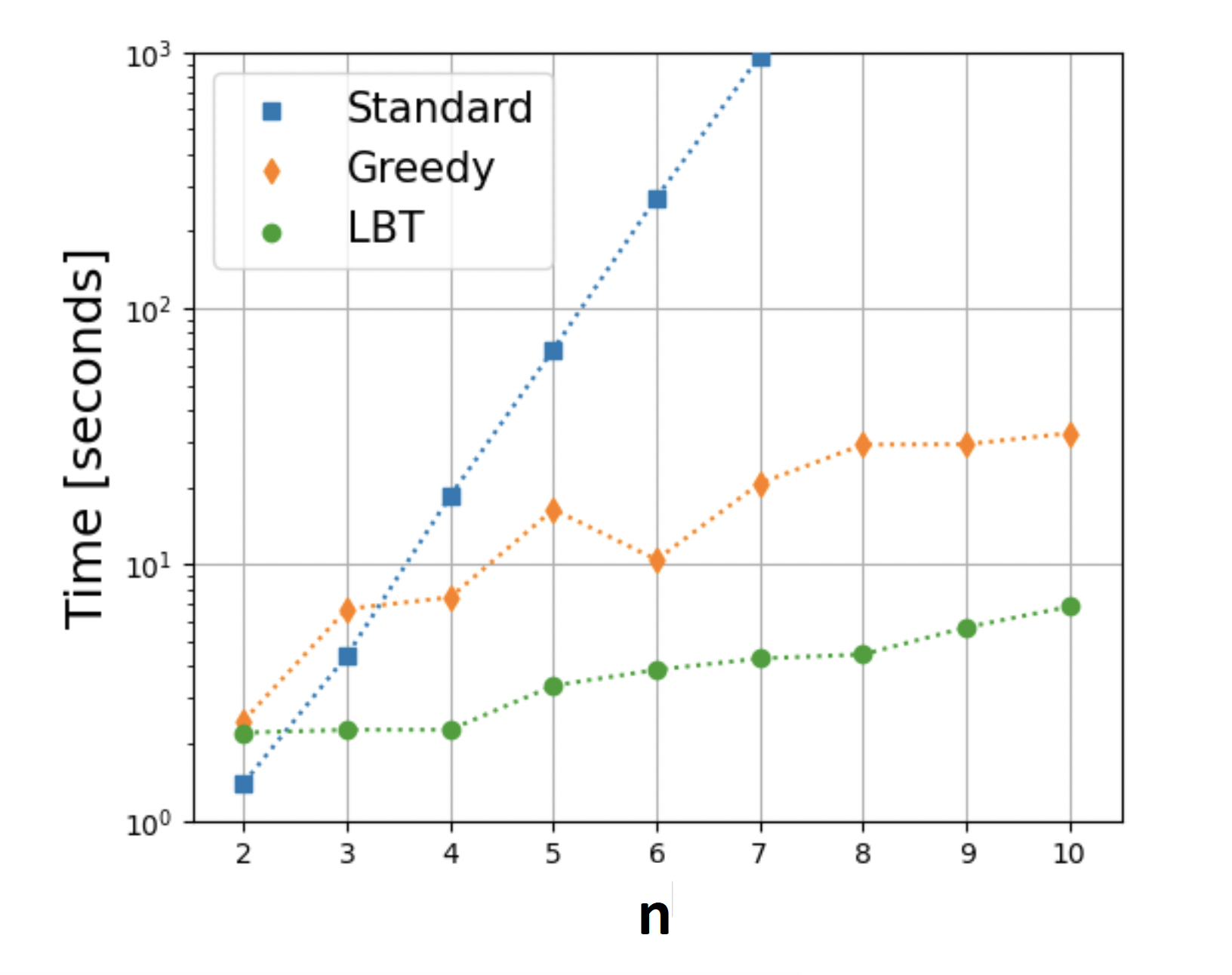Accelerated discovery of machine-learned symmetries: Deriving the exceptional Lie groups G2, F4 and E6

Roy T. Forestano, Konstantin T. Matchev, Katia Matcheva, and 3 more authors

Physics Letters B, Nov 2023

Abs PDF

Recent work has applied supervised deep learning to derive continuous symmetry transformations that preserve the data labels and to obtain the corresponding algebras of symmetry generators. This letter introduces two improved algorithms that significantly speed up the discovery of these symmetry transformations. The new methods are demonstrated by deriving the complete set of generators for the unitary groups U(n) and the exceptional Lie groups G2, F4, and E6. A third post-processing algorithm renders the found generators in sparse form. We benchmark the performance improvement of the new algorithms relative to the standard approach. Given the significant complexity of the exceptional Lie groups, our results demonstrate that this machine-learning method for discovering symmetries is completely general and can be applied to a wide variety of labeled datasets.
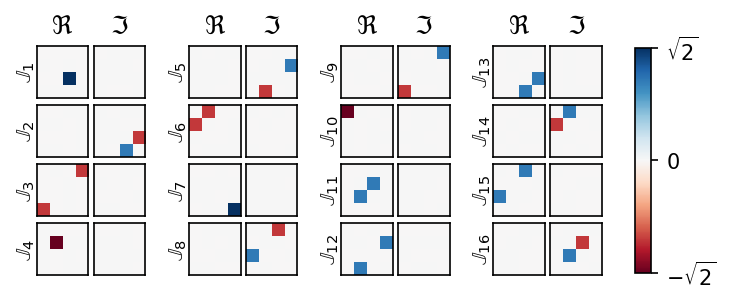Discovering sparse representations of Lie groups with machine learning

Roy T. Forestano, Konstantin T. Matchev, Katia Matcheva, and 3 more authors

Physics Letters B, Nov 2023

Abs PDF

Recent work has used deep learning to derive symmetry transformations, which preserve conserved quantities, and to obtain the corresponding algebras of generators. In this letter, we extend this technique to derive sparse representations of arbitrary Lie algebras. We show that our method reproduces the canonical (sparse) representations of the generators of the Lorentz group, as well as the U(n) and SU(n) families of Lie groups. This approach is completely general and can be used to find the infinitesimal generators for any Lie group.
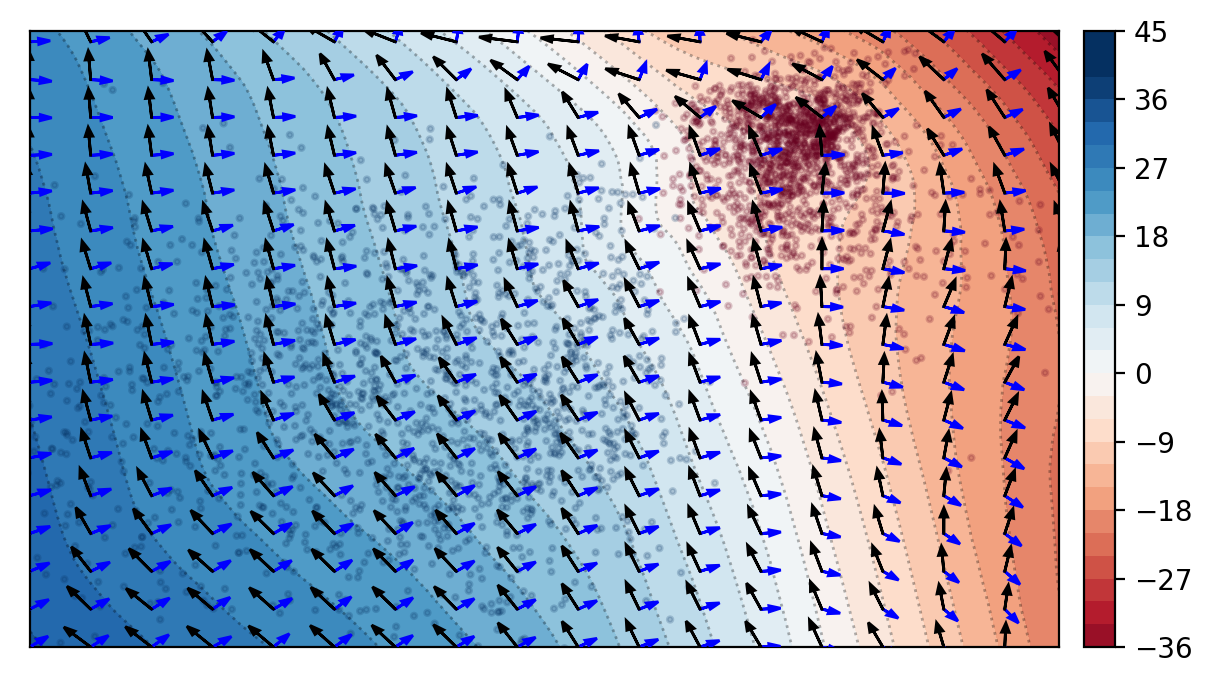Oracle-Preserving Latent Flows

Alexander Roman, Roy T. Forestano, Konstantin T. Matchev, and 2 more authors

Symmetry, Nov 2023

Abs PDF

A fundamental task in data science is the discovery, description, and identification of any symmetries present in the data. We developed a deep learning methodology for the simultaneous discovery of multiple non-trivial continuous symmetries across an entire labeled dataset. The symmetry transformations and the corresponding generators are modeled with fully connected neural networks trained with a specially constructed loss function, ensuring the desired symmetry properties. The two new elements in this work are the use of a reduced-dimensionality latent space and the generalization to invariant transformations with respect to high-dimensional oracles. The method is demonstrated with several examples on the MNIST digit dataset, where the oracle is provided by the 10-dimensional vector of logits of a trained classifier. We find classes of symmetries that transform each image from the dataset into new synthetic images while conserving the values of the logits. We illustrate these transformations as lines of equal probability (“flows”) in the reduced latent space. These results show that symmetries in the data can be successfully searched for and identified as interpretable non-trivial transformations in the equivalent latent space.
Deep learning symmetries and their Lie groups, algebras, and subalgebras from first principles

Roy T Forestano, Konstantin T Matchev, Katia Matcheva, and 3 more authors

Machine Learning: Science and Technology, Jun 2023

Abs PDF

We design a deep-learning algorithm for the discovery and identification of the continuous group of symmetries present in a labeled dataset. We use fully connected neural networks to model the symmetry transformations and the corresponding generators. The constructed loss functions ensure that the applied transformations are symmetries and the corresponding set of generators forms a closed (sub)algebra. Our procedure is validated with several examples illustrating different types of conserved quantities preserved by symmetry. In the process of deriving the full set of symmetries, we analyze the complete subgroup structure of the rotation groups SO(2), SO(3), and SO(4), and of the Lorentz group . Other examples include squeeze mapping, piecewise discontinuous labels, and SO(10), demonstrating that our method is completely general, with many possible applications in physics and data science. Our study also opens the door for using a machine learning approach in the mathematical study of Lie groups and their properties.

2022

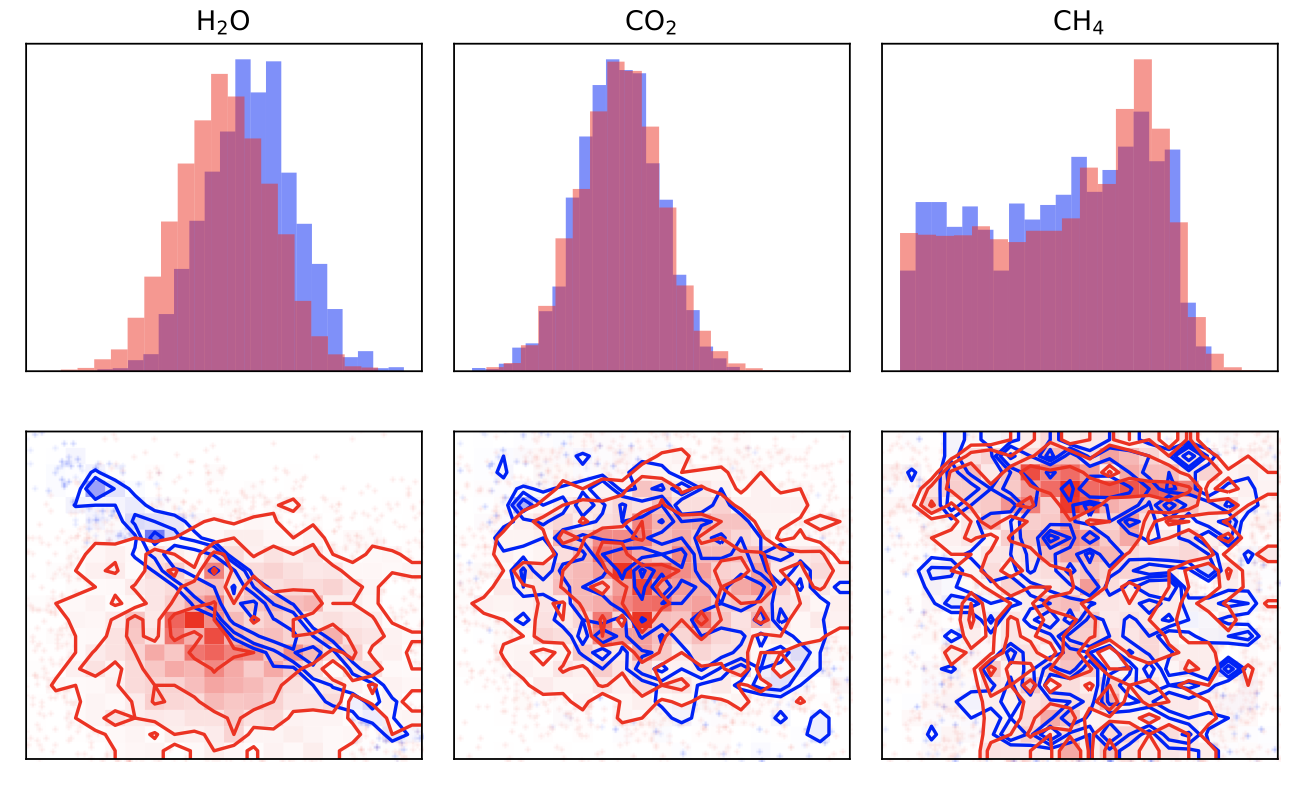Lessons Learned from Ariel Data Challenge 2022 - Inferring Physical Properties of Exoplanets From Next-Generation Telescopes

Kai Hou Yip, Quentin Changeat, Ingo Waldmann, and 19 more authors

In Proceedings of the NeurIPS 2022 Competitions Track, 28 nov–09 dec 2022

Abs PDF

Exo-atmospheric studies, i.e. the study of exoplanetary atmospheres, is an emerging frontier in Planetary Science. To understand the physical properties of hundreds of exoplanets, astronomers have traditionally relied on sampling-based methods. However, with the growing number of exoplanet detections (i.e. increased data quantity) and advancements in technology from telescopes such as JWST and Ariel (i.e. improved data quality), there is a need for more scalable data analysis techniques. The Ariel Data Challenge 2022 aims to find interdisciplinary solutions from the NeurIPS community. Results from the challenge indicate that machine learning (ML) models have the potential to provide quick insights for thousands of planets and millions of atmospheric models. However, the machine learning models are not immune to data drifts, and future research should investigate ways to quantify and mitigate their negative impact.